11286. В два
раза больше
Задан отсортированный массив A
из n целых чисел. Для каждого индекса i найдите, сколько
элементов в массиве лежит между Ai и 2 * Ai
включительно.
Вход. Первая строка содержит размер n
(n ≤ 105) массива A. Вторая строка содержит n целых
чисел в диапазоне от 0 до 109 в отсортированном порядке.
Выход. Выведите n чисел. Для
каждого индекса i (1 ≤ i ≤ n) массива выведите
количество элементов, лежащих между Ai и 2 * Аi включительно.
|
Пример
входа |
Пример
выхода |
|
10 1 2 3 4 5 6 7 8 9
10 |
2 3 4 5 6 5 4 3 2
1 |
РЕШЕНИЕ
два
указателя
Анализ алгоритма
Интервал A[i … j] будем
называть хорошим, если на нем находятся числа
в промежутке [Ai; 2 * Аi] включительно (то есть Aj ≤ 2 * Аi).
Реализуем скользящее
окно при помощи двух указателей i и j и будем его поддерживать так, чтобы текущий рассматриваемый интервал [i … j]
был хорошим, а интервал [i … j + 1] плохим.
Например, для
следующей последовательности
·
интервалы [2; 2], [2; 3], [2; 4] и [2; 5] являются хорошими.
·
интервалы [2; 6], [2; 7] являются плохими.
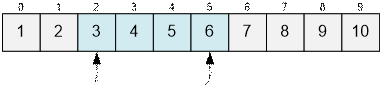
Если Aj ≤ 2 * Аi, то расширяем текущий интервал до А[i … j + 1]. Иначе сокращаем его до А[i + 1 … j]. Перед передвижением указателя i
выводим количество элементов, лежащих между Ai и 2 * Аi включительно. Оно равно j – i.
Оценка сложности
алгоритма линейная, то есть O(n).
Пример
Рассмотрим движение
указателей для приведенного примера.

Для заданного
состояния Aj ≤ 2 * Аi, поэтому двигаем вперед указатель j.
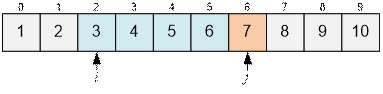
Теперь Aj > 2 * Аi. Вперед следует двигать указатель i. Однако перед его перемещением выводим количество элементов, лежащих
между Ai и 2 * Аi включительно.
Оно равно j – i = 6 – 2 = 4.
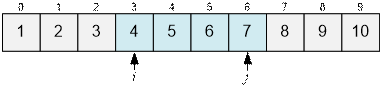
Двигаем j вперед пока Aj ≤ 2 * Аi.
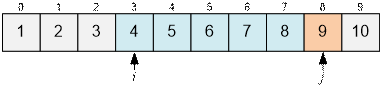
Теперь Aj > 2 * Аi. Выводим ответ для i = 3 (он равен j – i = 8 – 3 = 5) и увеличиваем i на 1.
Реализация алгоритма
Читаем входные
данные.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
Инициализируем указатели i = j = 0.
i = j = 0;
Двигаем указатели вперед пока для каждого значения i < n не будет найден
ответ.
while (i < n) // [i..j]
{
Если Aj ≤ 2 * Аi (но при этом j не вышло за границы
массива, то есть j < n), то расширяем текущий
интервал, увеличивая указатель j.
if ((j
< n) && (a[j] <= 2 * a[i])) j++;
else
{
При Aj > 2 * Аi выводим ответ для индекса i и увеличиваем i на единицу.
printf("%d ", j - i);
i++;
}
}
Реализация алгоритма – бинарный
поиск, O(n log n)
Читаем входные
данные.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);
Для каждого индекса i < n при помощи
бинарного поиска ищем такое наибольшее значение индекса x, что на
интервале [i;
x – 1] находятся числа от Аi до 2 * Аi, а Ax > 2 * Аi. Количество чисел на интервале [i; x – 1] равно x – i.
for (i = 0; i < n; i++)
{
x = upper_bound(v.begin(), v.end(), 2 * v[i]) - v.begin();
printf("%d ", x - i);
}
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m[] = new int[n];
for(int i = 0; i < n; i++)
m[i] = con.nextInt();
int i = 0, j = 0;
while (i < n) // [i..j]
{
if ((j < n)
&& (m[j] <= 2 * m[i])) j++;
else
{
System.out.print(j - i + "
");
i++;
}
}
con.close();
}
}
Python реализация
Читаем входные
данные.
n = int(input())
lst = list(map(int,input().split()))
Инициализируем указатели i = j = 0.
i = j = 0
Двигаем указатели вперед пока для каждого значения i < n не будет найден
ответ.
while (i < n): # [i..j]
Если Aj ≤ 2 * Аi (но при этом j не вышло за границы
массива, то есть j < n), то расширяем текущий
интервал, увеличивая указатель j.
if (j < n and lst[j] <= 2 * lst[i]):
j += 1
else:
При Aj > 2 * Аi выводим ответ для индекса i и увеличиваем i на единицу.
print(j - i, end=" ");
i += 1
Python реализация – бинарный поиск, O(n log n)
from bisect import bisect_right
Читаем входные данные.
n = int(input())
v = list(map(int, input().split()))
Для каждого
индекса i < n при помощи
бинарного поиска ищем такое наибольшее значение индекса x, что на
интервале [i; x – 1] находятся числа от Аi до 2 * Аi, а Ax > 2 * Аi. Количество чисел на интервале [i; x – 1] равно x – i.
for i in range(n):
x = bisect_right(v, 2 * v[i])
print(x - i, end=" ")